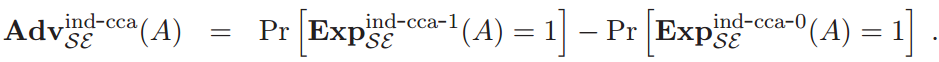Security of CBC with a random IV
مرصاد | پنجشنبه, ۱۱ آذر ۱۳۹۵، ۰۸:۱۶ ب.ظ
امنیت سبک زنجیرهای قالبهای رمز
رمزهای قالبی به تنهای دردی از ما دوا نمیکنند! همانطور
که میدانید یک خانواده از رمزهای قالبی زمانی ایدهال است که، یک خانواده
از جایگشتهای شبه تصادفی باشد. حتی اگر فرض کنیم که رمزهای قالبی نظیر AES
که امروزه مورد استفاده قرار میگیرند جایگشت شبه تصادفی هستند، با این
وجود ممکن است طوری از آن برای رمزکردن دادههای بزرگ استفاده شود که امنیت
مورد انتظار برآورده نشود. میدانیم که دو پارامتر مهم رمزهای قالبی ۱)
طول قالب داده و ۲) طول کلید هستند. طول قالب داده در رمزهای قالبی محدود
است و در اغلب موارد طول دادهای که قرار است رمز شود از طول قالب داده در
رمز قالبی بزرگتر است. بنابراین گام بعد از طراحی یک رمزقالبی خوب، طراحی
فرآیند استفاده امن از آن رمز قالبی برای رمز کردن دادههایی با طول بیشتر
از طول قالب داده است.
بیایید فرض کنیم گام اول به درستی برداشته شده و ما یک
رمزقالبی که یک جایگشت شبه تصادفی است را در اختیار داریم. به انحا مختلف
میتوانیم از این رمز قالبی برای رمز کردن دادههایی با طول دلخواه استفاده
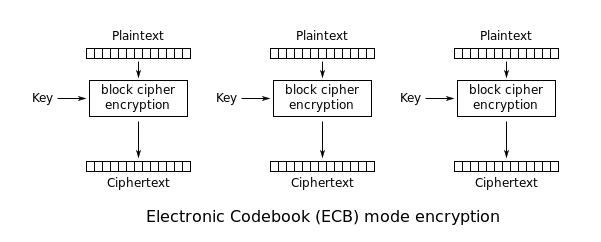
کنیم، برای مثال فرض کنید از مد کاری نشان داده شده در شکل زیر که به مد
کاری ECB معروف است استفاده کنیم.
خوب! نتیجه رمزنگاری تصویر لوگوی لینوکس با مد کاری ECB را در زیر مشاهده فرمایید.
همانطور که مشاهده میکنید داده رمزشده اطلاعات بسیاری
از تصویر اصلی بهدست میدهد و این اصلا خوب نیست! این امر دور از انتظار
نبود چون مد کاری ECB یک مد کاری کاملا قطعی (deterministic) است و لذا
دارای امنیت متن اصلی انتخابی نیست. این مد کاری حتی دارای امنیت تکپیامی
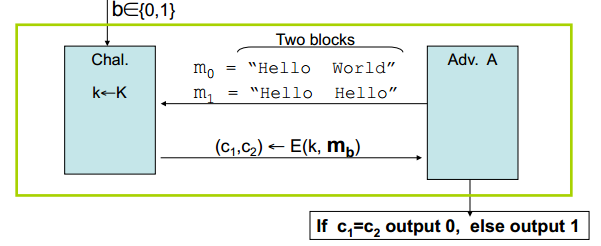
هم نیست چرا که اگر دو قالب از متن اصلی با هم یکسان باشند، قالبهای
متناظر آنها در متن رمزشده نیز یکسان هستند، بنابراین همانطور که در شکل
زیر نمایش داده شده، بهراحتی میتوانیم رمزشده یک متن اصلی که حاوی دو
بلوک مشابه است را از رمزشده یک متن که حاوی دو بلوک متفاوت است تمیز دهیم.
برای دیدن مدهای کاری بیشتر و البته جدیدتر، بنگرید به
اما مد کاری که قصد داریم در اینجا راجع به آن بحث کنیم مد کاری CBC است که نحوهی رمزنگاری و رمزگشایی در این مد کاری در شکلهای زیر نشان داده شده است.
فرض کنید طول قالب رمز قالبی E برابر n باشد، در اینصورت الگوریتم رمزنگاری و رمزگشایی بهصورت زیر است. (برگرفته از کتاب مقدمهای بر رمزنگاری مدرن نوشته دو یار همیشگی! Mihir bellare و Phillip rogaway.)
(لطفا فعلا پدینگ را بیخیال شوید!) در الگوریتم فوق هم فرض براین است که طول متن اصلی مضربی از طول قالب است و اگر این طور نباشد الگوریتم bot برمیگرداند. در ضمن برای IV دوحالت میتوان در نظر گرفت، یک حالت این است که در هر بار رمزنگاری آن را بهصورت تصادفی تعیین کنیم (که الگوریتم بالا از این نوع است) و نوع دیگر این است که آن را به صورت یک شمارنده در نظر بگیریم که در هر بار عمل رمزنگاری یکواحد افزایش مییابد. سؤال این است که اگر رمز قالبی ما یک جایگشت شبهتصادفی باشد و IV بهصورت تصادفی در نظر گرفته شود، آیا مد کاری CBC امنیت CPA را برآورده میکند؟ امنیت CCA را چطور؟
پاسخ نهایی این است که اگر در هر بار عمل رمزنگاری IV بهصورت تصادفی تعیین شود، این مد کاری امنیت CPA دارد ( رجوع کنید به مقدمهای بر رمزنگاری مدرن نوشته Katz و Lindell ویرایش ۲ صفحه ۹۰) ولی دارای امنیت CCA نیست و وقتی IV به صورت شمارندهای تعیین شود حتی امنیت CPA هم نداریم. اما چطور میتوان ثابت کرد؟ قبل از هر چیز بیایید مفهوم تابع و جایگشت شبهتصادفی و آزمایش امنیت CPA و امنیت CCA و مفهوم مزیت مهاجم در هر یک از این آزمایشها را باهم مرور کنیم. ابتدا آزمایش (یا بازی) حمله متن اصلی انتخابی را مرور میکنیم.
مرور مفاهیم پایه
ما در این بخش به مروز مفاهیم پایه مورد نیاز این بحث
میپردازیم تا ضمن یادآوری، در طریق نمادگذاریها به یک اتحاد و تفاهم
برسیم و معنای هر یک از نمادهای بهکار رفته واضح باشد.
تابع شبه تصادفی
فرض کنید مجموعههای D و R را بهترتیب به عنوان دامنه و
برد در نظر بگیریم. به بیان نادقیق تابع شبه تصادفی از D به R به
خانوادهای از توابع از D به R گفته میشود که رفتار ورودی و خروجی یک عضو
آن (که با توزیع یکنواخت انتخاب شده) از رفتار یک تابع که به تصادف از بین
کل توابع ممکن از D به R انتخاب شده است، تمایزناپذیر محاسباتی باشد. در
ضمن دامنه و برد در اغلب مباحث رمزنگاری همان مجموعه رشتههای n بیتی است.
حال تصور کنید در اتاقی هستید که به یک ترمینال ( برای ویندوزیها همان کامند پرامپت!) که به یک کامپیوتر خارج از اتاق شما وصل است دسترسی دارید. شما فقط میتوانید عضوی از دامنه D را در ترمینال تایپ کنید و سپس جواب یا مقدار تابع بهوسیله کامپیوتر خارج از اتاق محاسبه شده و به شما و در همان ترمینال نمایش داده میشود. آنچه کامپیوتر محاسبه میکند و بازمیگرداند مقدار یک تابع مثل g به ازای ورودی ارسالی از جانب شما است. تابع g بهوسیله کامپیوتر و به دو طریق ممکن انتخاب میشود.
حالت ۰) تابع g به تصادف و با توزیع یکنواخت از بین تمام توابع از D به R یعنی 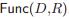 انتخاب میشود. (جهان صفر)
انتخاب میشود. (جهان صفر)
حالت ۱) تابع g به تصادف و با توزیع یکنواخت، ولی اینبار از خانوادهای از
توابع از D به R مثل F که با اندیس k (کلید) پارامتری شده انتخاب
میشود. دقت کنید که F زیر مجموعهای از 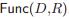 است. (جهان یک)
است. (جهان یک)
راجع به اینکه کامپیوتر بیرون اتاق بر اساس کدامیک از
حالات فوق تابع را انتخاب کرده است، به شما چیزی گفته نمیشود. کامپیوتر
یک تابع را بر اساس یکی از حالات فوق انتخاب میکند و سپس شما با دیدن فقط
ورودی و خروجیهای آن باید حدس بزنید تابع بر اساس کدام حالت انتخاب شده
است، حالت ۰ یا حالت ۱؟ شما فقط ورودیها را تعیین میکنید و بلافاصله
خورجی متناظر با آن را مشاهده میکنید، در این حالت اصطلاحا میگوییم که
شما به تابع انتخاب شده دسترسی اوراکلی دارید.
فرض کنید 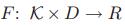 یک خانواده از توابع و A الگوریتم تمایزگر باشد که به تابع انتخاب شده از خانواده F (یا از بین کل توابع ممکن
یک خانواده از توابع و A الگوریتم تمایزگر باشد که به تابع انتخاب شده از خانواده F (یا از بین کل توابع ممکن 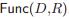 ؟؟؟) دسترسی اوراکلی دارد و خروجی آن (به منزله حدس این که تابع بر اساس
کدام حالت انتخاب شده) یا صفر و یا یک است (که با b نمایش میدهیم.) دو
آزمایش زیر را در نظر بگیرید.
؟؟؟) دسترسی اوراکلی دارد و خروجی آن (به منزله حدس این که تابع بر اساس
کدام حالت انتخاب شده) یا صفر و یا یک است (که با b نمایش میدهیم.) دو
آزمایش زیر را در نظر بگیرید.
در اینصورت مزیت الگوریتم تمایزگر A عبارت است از
البته درستتر آن است که قدر مطلق عبارت فوق را مزیت در نظر بگیریم ولی برای سادگی از قدر مطلق صرف نظر شده است. حال اگر مزیت هر الگوریتم تمایزگر چندجملهای تصادفی در تمایز خانواده توابع داده شده از کل توابع از D به R، ناچیز باشد، آن خانواده را شبه تصادفی گوییم. به بیان نادقیق اگر برای خانواده توابع داده شده، مزیت هر تمایزگر (چندجملهای تصادفی) ناچیز باشد آنخانواده شبه تصادفی خواهد بود.
در تعریف مزیت تحت حمله متن اصلی انتخابی برای جایگشت شبه تصادفی فرض کنید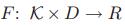 خانوادهای از جایگشتها روی D باشد. همچنین فرض کنید A الگوریتم
تمایزگری است که به جایگشت انتخاب شده دسترسی اوراکلی دارد و خروجی آن یا
صفر و یا یک است. دو آزمایش زیر را در نظر بگیرید.
خانوادهای از جایگشتها روی D باشد. همچنین فرض کنید A الگوریتم
تمایزگری است که به جایگشت انتخاب شده دسترسی اوراکلی دارد و خروجی آن یا
صفر و یا یک است. دو آزمایش زیر را در نظر بگیرید.
که در آن Perm(D) مجموعه همه جایگشتها روی D است. در اینصورت cpa-مزیت تمایزگر A بهصورت زیر تعریف میشود.
خانوداه F از جایگشتها زمانی یک خانواده
جایگشت شبه تصادفی امن تحت CPA (حمله متن اصلی انتخابی) است که مزیت فوق
برای هر تمایزگر (چندجملهای تصادفی) ناچیز باشد.
اکنون فرض کنید به تمایزگر فوق دسرتسی اوراکلی به معکوس تابع انتخاب شده را نیز بدهیم، دو آزمایش زیر را در نظر بگیرید.
در اینصورت CCA-مزیت تمایزگر A بهصورت زیر تعریف میشود.
در اینحالت نیز اگر به ازای هر تمایزگر (چندجملهای تصادفی) مزیت فوق ناچیز باشد، خانواده جایشگتهای داده شده یک جایگشت شبه تصادفی امن تحت CCA(حمله متن رمزی انتخابی) خواهد بود. در برخی کتابها نظیر کتاب کتز و لیندل به خانواده جایشگتهایی که شبه تصادفی امن تحت CCA باشند، جایگشت شبه تصادفی گفته میشود که در این حالت مفهوم امنیت خانواده جایگشت داده شده در عبارت شبهتصادفی مستتر است و به طور خلاصه میگوییم خانواده جایگشت داده شده یک جایگشت شبه تصادفی است.
امنیت CPA و CCA
فرض کنید 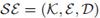 یک سامانه رمزنگاری متقارن باشد. همچنین فرض کنید A الگوریتمی باشد که به اورکل رمزنگاری (متن چپ یا راست)
یک سامانه رمزنگاری متقارن باشد. همچنین فرض کنید A الگوریتمی باشد که به اورکل رمزنگاری (متن چپ یا راست) 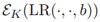 دسترسی دارد. دو آزمایش زیر را در نظر بگیرید.
دسترسی دارد. دو آزمایش زیر را در نظر بگیرید.

در اینصورت مزیت الگوریتم A در حمله متن اصلی انتخابی بهصورت زیر تعریف میشود.
در ضمن، اوراکل رمزنگاری (یا اوراکل Left Or Right encription- LOR) به صورت زیر عمل میکند.
خوب، حالا بیایید آزمایش حمله متن رمزی انتخابی یا CCA و مفهوم مزیت
الگوریتم مهاجم در آن را با هم مرور کنیم. با همان فرضیات قبلی آزمایش زیر
را در نظر بگیرید.
در اینصورت مزیت A در حمله متن اصلی انتخابی بهصورت زیر تعریف میشود.
اگر این مفاهیم را از کتاب Katz و Lindell خوانده باشید میدایند که نمادگذاریهای این کتاب کمی با نمادگذاریهای فوق متفاوت است اما این تفاوتها تفاوتهای بنیادی نیستند و فقط ظاهر قضیه کمی متفاوت است. در ضمن Katz و Lindell در کتاب خود، در بسیاری از موارد به مقاله های Bellare و Rogaway ارجاع دادهاند.
در ادامه نشان میدهیم که مد کاری CBC با IV تصادفی که با جایگشت شبه
تصادفی ساخته شده است، CPA- امن است. قبل از آن باید چند لم را ثابت کنیم.
- ۰ نظر
- ۱۱ آذر ۹۵ ، ۲۰:۱۶